David Hernandez: Shifted quantum affine algebras, monoidal categorication and Langlands duality

David Jordan | Langlands duality for 3 manifoldsSee more

Quantum Affine Algebras and Cluster Algebras Pt. 1See more

David Hernandez: Folded quantum integrable models and deformed W-algebrasSee more

Langlands duality for quantum affine algebras &See more

Quantum Affine Algebras and Cluster Algebras Pt. 2See more

Spectra of quantum KdV Hamiltonians, Langlands duality and category O, By: David HernandezSee more

The Fundamental Local Equivalence in quantum geometric LanglandsSee more

WHCGP: Davide Gaiotto, "Integrable Kondo problems and affine Geometric Langlands"See more

D. Gaitsgory - "fundamental local equivalence" for quantum geometric LanglandsSee more

Quantum Affine Algebras and their Finite Dimensional Representations - Nicolai ReshetikhinSee more

Affine quantum groups Lecture 1See more
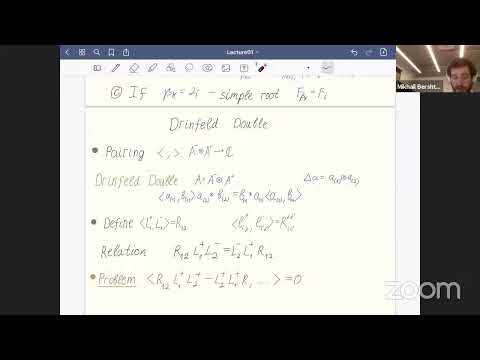
Perfect crystals for quantum affine algebras and combinatorics of Young wallsSee more
